Explains the need for Normalization and the general techniques used

Why Normalization helps

Let’s first understand the problem with Covariate Shift and how normalization techniques help overcome it.

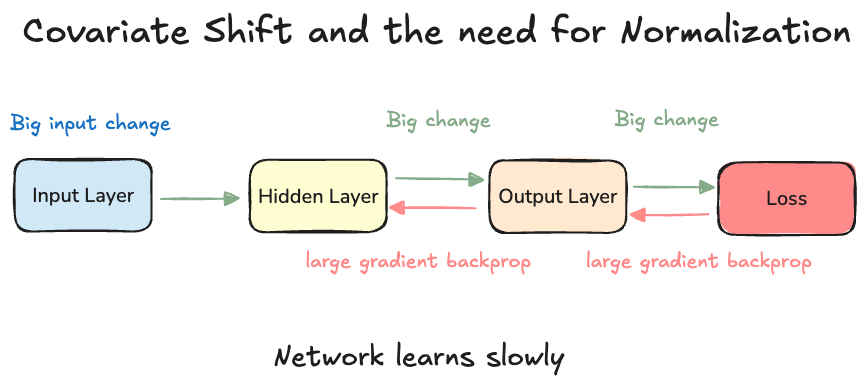
What is the Covariate shift problem

• Big changes in the input propagate through the network
• Leads to larger loss, larger gradient and larger weight updates.
• Slows down the network

What should we do

• Standardize the inputs to each layer
• Reduce the dependence of each layer on the scale of its inputs
• Allow each layer to learn more independently of others

This results in:

• Faster and more stable training
• Improved generalization
• Reduced sensitivity to initialization

By addressing covariate shift, normalization techniques like Batch Normalization, Layer Normalization, and RMS Normalization have become essential components in modern deep learning architectures.

What is Normalization

We calculate some stats about the input can adjust the input accordingly

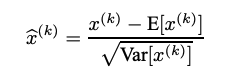
The Two main stats are μ and σ

Batch Normalization

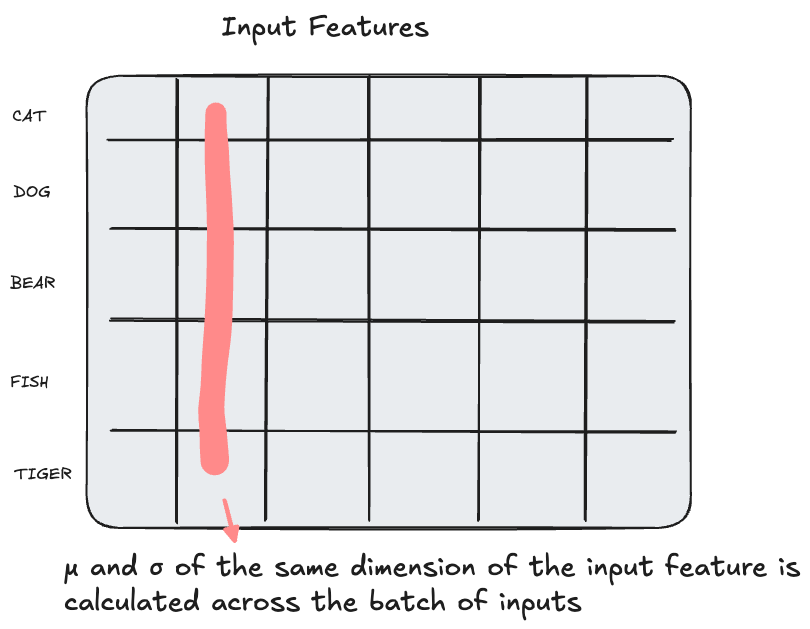
Statistics such as μ and σ are calculated across the same dimension of the batch of inputs. This is used to adjust the values of the input to be standard.

Reference: paper

Layer Normalization

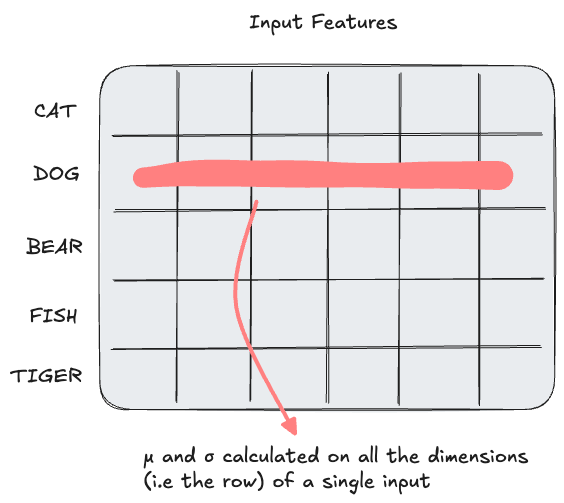
Layer Norm equation is as follows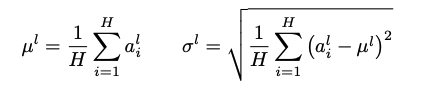

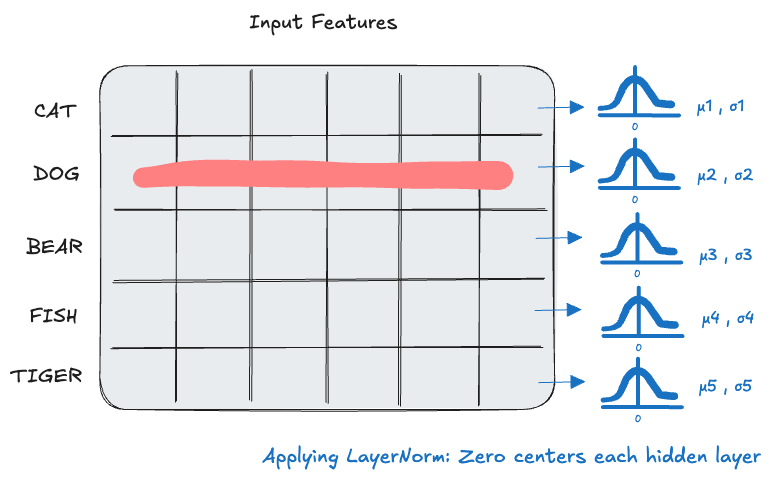
Layernorm uses the row as is input to calculate the μ and σ. This is reduces dependence of each layer on the scale of its inputs.

Reference: paper

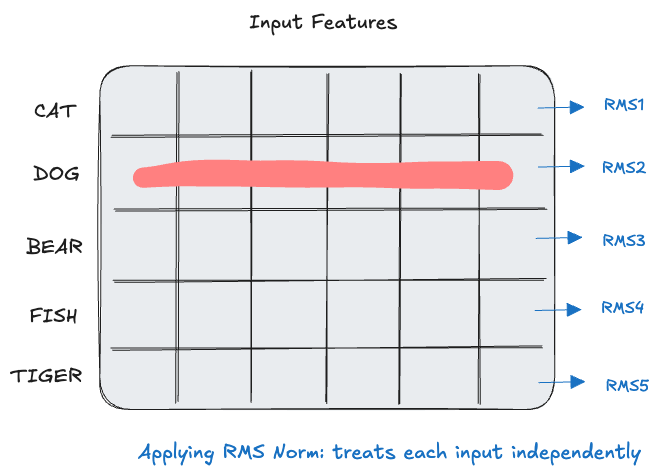
RMS Normalization

This is an improvement over LayerNorm. The Authors

1. Hypothesize that the re-scaling invariance is the reason for success of LayerNorm, rather than re-centering invariance
2. Use RMS (root mean square) statistic
3. Lesser number of computations
4. Simplify LayerNorm by removing the mean statistic